2017 年的 RoboMaster 比赛中,基地区域周围有八个二维码,可以用于定位。本文介绍一种基于三点定位得到无人机相对基地坐标的方法。

提取二维码
基地所用的二维码类型为 AprilTag,来自密西根大学,BSD 协议发布,调用 AprilTag 的库就可以识别出二维码。
cv::cvtColor(src, image_gray, CV_BGR2GRAY);
detections = m_tagDetector->extractTags(image_gray);
转换成灰度图后调用 TagDetector 的 extractTags 方法,提取到的二维码信息就返回到 vector<AprilTags::TagDetection> 类型的detections中了。
二维码信息处理
接下来就是要利用这些信息,得到相机在地面上的投影距离各二维码的距离了。
/* tag coordinates to ground, origin point is in the center
* same coordinate as uav
* x -- up arrow
* y -- right arrow
*/
static cv::Point2f id2location[12] = {
cv::Point2f(-0.85, 0.85), cv::Point2f(-0.85, 0.00), cv::Point2f(-0.85, -0.85),
cv::Point2f(0.00, 0.85), cv::Point2f(0.00, -0.85), cv::Point2f(0.85, 0.85),
cv::Point2f(0.85, 0.00), cv::Point2f(0.00, 0.00), cv::Point2f(0.00, 0.00),
cv::Point2f(0.00, 0.00), cv::Point2f(0.85, -0.85)
};
/* distance from camera's shadow to origin point */
float shadow_distance;
/* find the right id tags and get the distance
* from camera's shadow on ground to tag
*/
for(int i = 0; i < detections.size(); i++)
{
if(detections[i].hammingDistance != 0)
continue;
if(!((detections[i].id >= 0 && detections[i].id <= 6) ||
detections[i].id == 10))
continue;
shadow_location.push_back(id2location[detections[i].id]);
Eigen::Vector3d translation;
Eigen::Matrix3d rotation;
detections[i].getRelativeTranslationRotation(m_tagSize, m_fx, m_fy, m_px,
m_py, translation, rotation);
shadow_distance=
sqrt(abs(pow(translation.norm(), 2) - pow(height, 2)));
shadow_radius.push_back(shadow_distance);
}
在 shadow_location 和 shadow_radius 中分别储存了,提取到的二维码在地面坐标系的坐标,以及相机投影的距离。投影就在这样一个以该坐标为圆心,该距离为半径的圆上。
其中,距离的计算需要无人机的高度来通过直线距离算出投影距离,需要高度反馈或确定的高度。而直线距离又需要相机的相关参数和二维码的尺寸来计算,这些需要事先测量。
三圆定点
已知三个圆,理论上是可以定出点的坐标的。
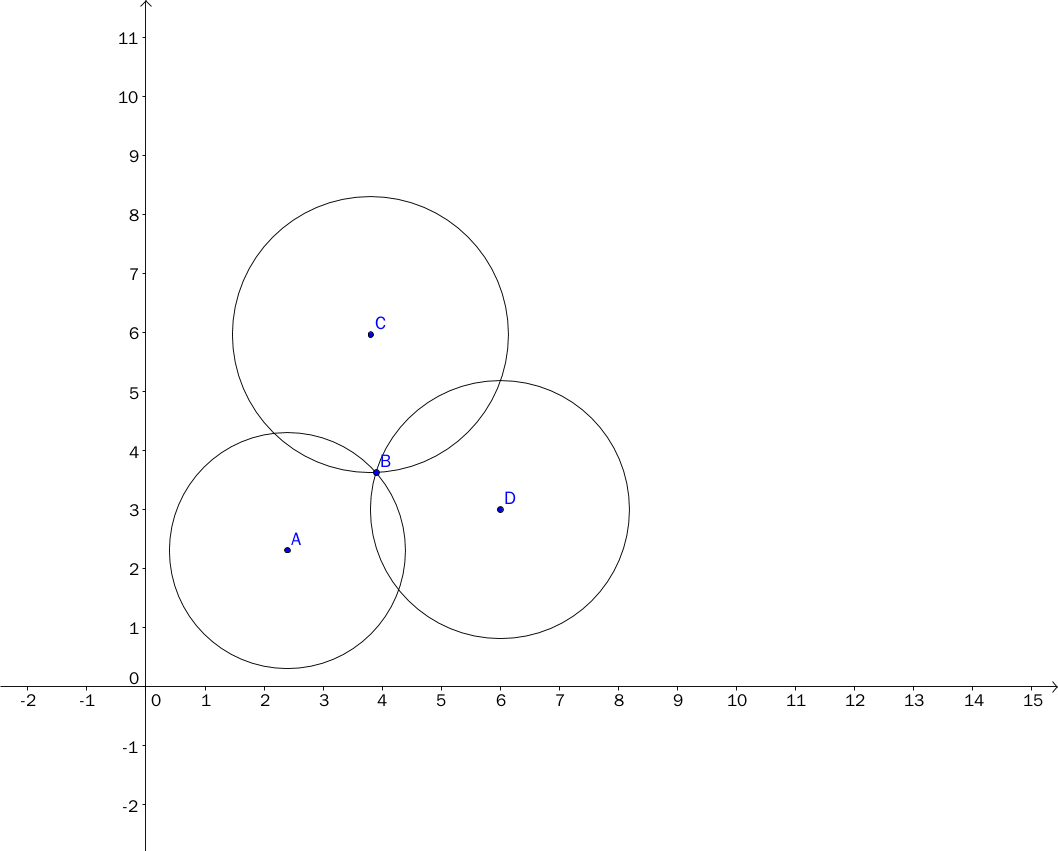
但是实际使用中测量会有误差,所以三圆往往不是交于一点,而是形成一个小区域。比较好的估算方式是选取小区域的中心点。
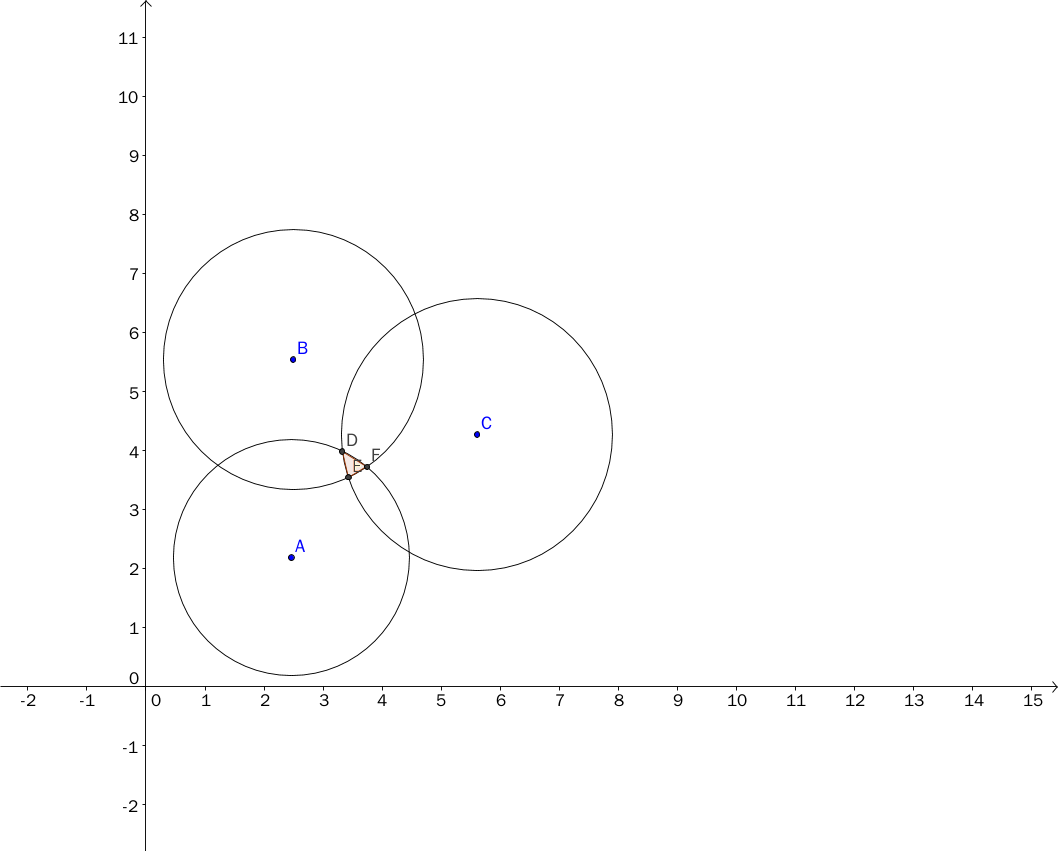
我的具体方法如下图,选择三条公共割线的交点作为坐标:
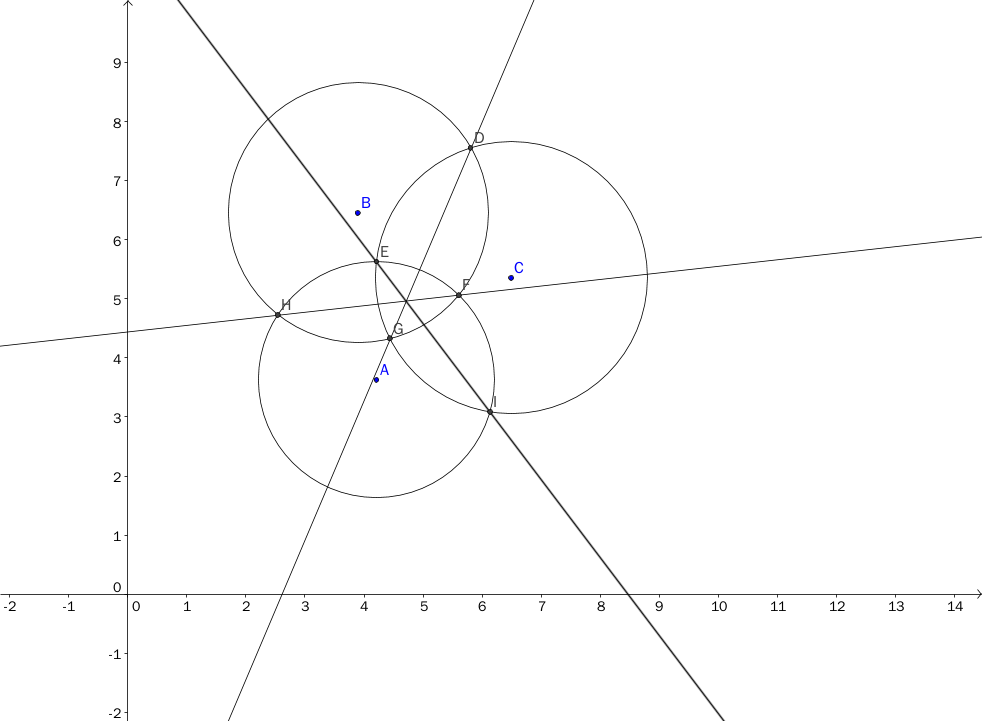
公共割线的方程可以通过圆的方程相减得到。由于三条线交于一点,只要计算两条线的交点就可以了,可以用行列式求解,公式推导如下:
有三个圆,圆心坐标分别为$(x_1,y_1),(x_2,y_2),(x_3,y_3)$,半径分别为$r_1,r_2,r_3$
\[Circle 1: (x - x_1)^2+(y - y_1)^2 = r_1^2 \quad (1) \\ Circle 2: (x - x_2)^2+(y - y_2)^2 = r_2^2 \quad (2) \\ Circle 3: (x - x_3)^2+(y - y_3)^2 = r_3^2 \quad (3) \\\]$(2)-(1),(3)-(2)$得:
\[2(x_2 - x_1)x+2(y_2 - y_1)y = r_1^2 - r_2^2 + x_2^2 - x_1^2 + y_2^2 - y_1^2 \\ 2(x_3 - x_2)x+2(y_3 - y_2)y = r_2^2 - r_3^2 + x_3^2 - x_2^2 + y_3^2 - y_2^2\]令$C_1 = r_1^2-r_2^2+x_2^2-x_1^2+y_2^2-y_1^2$
$C_2 = r_2^2-r_3^2+x_3^2-x_2^2+y_3^2-y_2^2$
方程简化为:
\[2(x_2 - x_1)x+2(y_2 - y_1)y = C_1 \\ 2(x_3 - x_2)x+2(y_3 - y_2)y = C_2\]利用行列式求线性方程组:
\[D = \begin{vmatrix} 2(x_2 - x_1) & 2(y_2 - y_1) \\ 2(x_3 - x_2) & 2(y_3 - y_2) \\ \end{vmatrix} \\ D_x = \begin{vmatrix} C_1 & 2(y_2 - y_1) \\ C_2 & 2(y_3 - y_2) \\ \end{vmatrix} \\ D_y = \begin{vmatrix} 2(x_2 - x_1) & C_1 \\ 2(x_3 - x_2) & C_2 \\ \end{vmatrix}\] \[x = \frac{D_x}{D} \\ y = \frac{D_y}{D}\]具体代码实现如下:
float x1= Point1.x, x2= Point2.x, x3= Point3.x;
float y1= Point1.y, y2= Point2.y, y3= Point3.y;
float D= 2 * ((x2 - x1) * (y3 - y2) - (y2 - y1) * (x3 - x2));
float C1= radius1 * radius1 - radius2 * radius2 + x2 * x2 - x1 * x1 +
y2 * y2 - y1 * y1;
float C2= radius2 * radius2 - radius3 * radius3 + x3 * x3 - x2 * x2 +
y3 * y3 - y2 * y2;
float Dx= C1 * (y3 - y2) - C2 * (y2 - y1);
float Dy= C2 * (x2 - x1) - C1 * (x3 - x2);
float centerPoint_x= Dx / D, centerPoint_y= Dy / D;
那么当三圆交不到一起的情况呢?
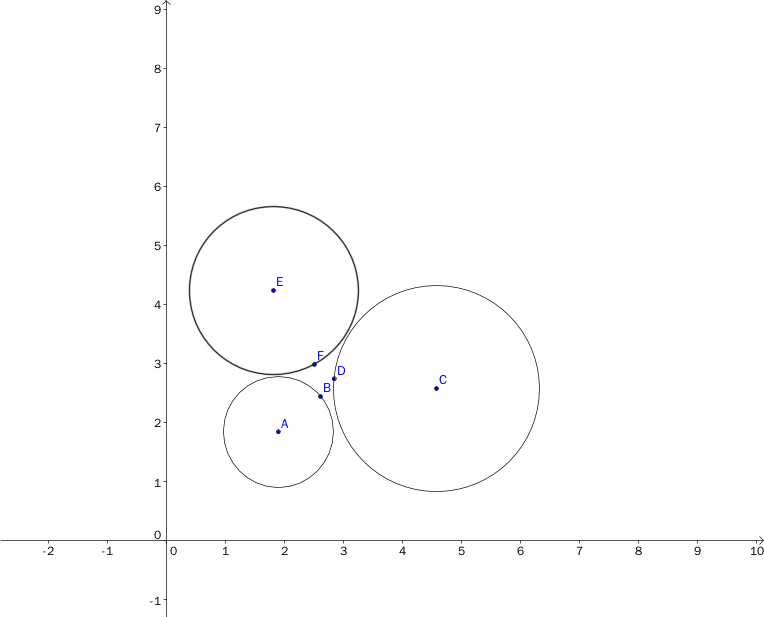
不用担心,这个算法依然能估算出中心点。此时,圆方程相减得到的直线方程是两圆公共切线中点的连线。详细证明链接在此,感兴趣的读者可以下载阅读。
为了减小误差,要尽量用到所有圆的信息:
cv::Point2f centerPoint;
vector<cv::Point2f> centerPoints;
// get centerpoint(s) of all circles
for(int i= 0; i < shadow_location.size() - 2; i++)
{
for(int j= i + 1; j < shadow_location.size() - 1; j++)
{
for(int k= j + 1; k < shadow_location.size(); k++)
{
if(calculateCenterPointFrom3Circles(
shadow_location[i], shadow_radius[i],
shadow_location[j], shadow_radius[j],
shadow_location[k], shadow_radius[k], centerPoint))
{
centerPoints.push_back(centerPoint);
}
}
}
}
float x_sum= 0, y_sum= 0;
for(int i= 0; i < centerPoints.size(); i++)
{
x_sum+= centerPoints[i].x;
y_sum+= centerPoints[i].y;
}
centerPoint.x= x_sum / centerPoints.size();
centerPoint.y= y_sum / centerPoints.size();
计算了所有可能的情况,得到一系列中心点,再对其求平均,就可以估算出比较精确的值了。实际使用中,能达到 0.1米 的精度。
计算方向
无人机长时间飞行后,水平方向的朝向会有一定角度的偏移,如果不校准的话,每次向前飞都会歪,影响控制。基地上空的二维码就提供了一个地标,可以用来测量偏移的角度。
计算原理是通过二维码连成的直线在图像极坐标系(即相机坐标系)和地面极坐标系里的偏移角度之差,算出相机和地面的偏移角度。
/* id=2 tag as origin point
* same coordinate as opencv
* x -- right arrow
* y -- down arrow
*/
static cv::Point2f id2location[12]= {
cv::Point2f(1.9, 1.9), cv::Point2f(1.05, 1.9), cv::Point2f(0.2, 1.9),
cv::Point2f(1.9, 1.05), cv::Point2f(0.2, 1.05), cv::Point2f(1.90, 0.2),
cv::Point2f(1.05, 0.2), cv::Point2f(0.0, 0.0), cv::Point2f(0.0, 0.0),
cv::Point2f(0.0, 0.0), cv::Point2f(0.2, 0.2)
};
/* calculate each two-tag line's degree
* in the ground coordinate and image coordinate.
* And sub two degree to get camera's rotation to ground
*/
float tag_vector_x, tag_vector_y, tag_alpha,
img_vector_x, img_vector_y, img_beta;
float degree;
vector< float > degrees;
for( int i=0; i < detections.size()-1; i++)
{
for(int j=i+1; j<detections.size(); j++)
{
if(detections[j].hammingDistance != 0 ||
!( (detections[j].id >= 0 &&
detections[j].id <= 6) ||
detections[j].id == 10) )
continue;
tag_vector_x = id2location[detections[j].id].x
- id2location[detections[i].id].x;
tag_vector_y = id2location[detections[j].id].y
- id2location[detections[i].id].y;
img_vector_x = detections[j].cxy.first
- detections[i].cxy.first;
img_vector_y = detections[j].cxy.second
- detections[i].cxy.second;
tag_alpha = atan2(tag_vector_x, tag_vector_y)*180/PI;
img_beta = atan2(img_vector_x, img_vector_y)*180/PI;
degree = img_beta - tag_alpha;
degrees.push_back(degree);
}
}
同样的,为了减小误差,要计算所有可能的直线。最后再求平均值,就可以估算出较精确的偏移角度。实际使用中,精确度能达到 1 度。
总结
RoboMaster 基地区没有黄线,只能依靠二维码定位,经典的三圆定点方法很有效。同时,也可以借助二维码来校正方向。利用地面上二维码的时候,主要是分清地面坐标系和相机坐标系,这样就可以得到想要的信息了。

