RoboMaster 2019 击打小陀螺
在RoboMaster 2018赛季,中国矿业大学的小陀螺横空出世,并且在赛季结束后开源了他们的方案。在 2019 赛季,小陀螺几乎成了强队的标配。不断旋转的底盘给准确击打装甲板造成了极大的困难。步兵机器人尚且可以依靠连续发射来造成伤害,但是对于一次只能发射一颗大弹丸的英雄机器人,必须提高击打的效率。方便起见,这里只研究击打原地旋转的小陀螺。
之前我介绍过了打击哨兵的方案,使用线性回归预测哨兵的运动。小陀螺也需要预测,但是和哨兵的运动差别很大:
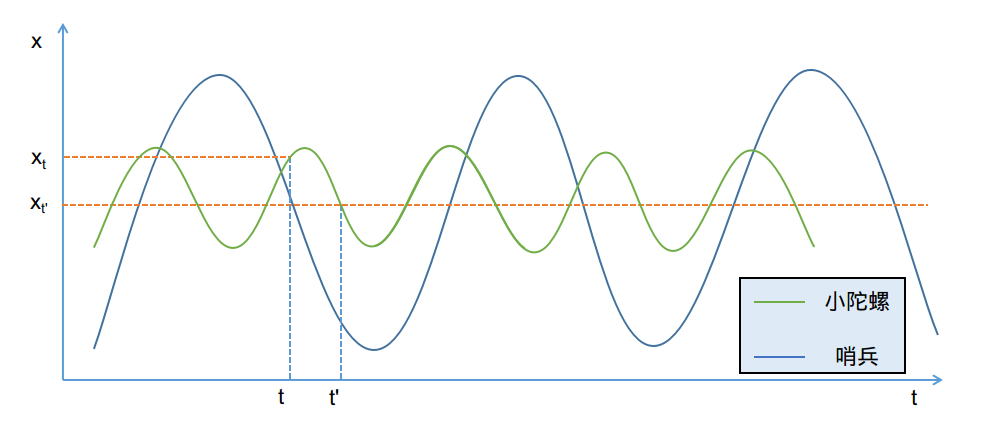
如图,蓝色线代表哨兵的运动,绿色线代表小陀螺的运动。第一个区别在于周期,哨兵完整地巡逻需要好几秒,但是小陀螺转一圈只需要一秒,周期远小于哨兵。第二个区别在于运动幅度,哨兵的轨道长达几米,而小陀螺的装甲板只会在一米范围内旋转。这就意味着,不能把小陀螺的运动近似成线性的。比如,同样在t时刻观测,哨兵在t‘的位置可以用线性回归预测,小陀螺就不可以了。
因此,反小陀螺的主要难点在于,当视觉识别到当前装甲板的时候,已经来不及击打这个装甲板了,因此需要在更长的时间维度上建模,也就是需要测量周期。
测量周期的办法有很多。理论上最稳定的办法是通过傅里叶变换找到频域里的峰值。然而,实际识别到的位置信号是这样的: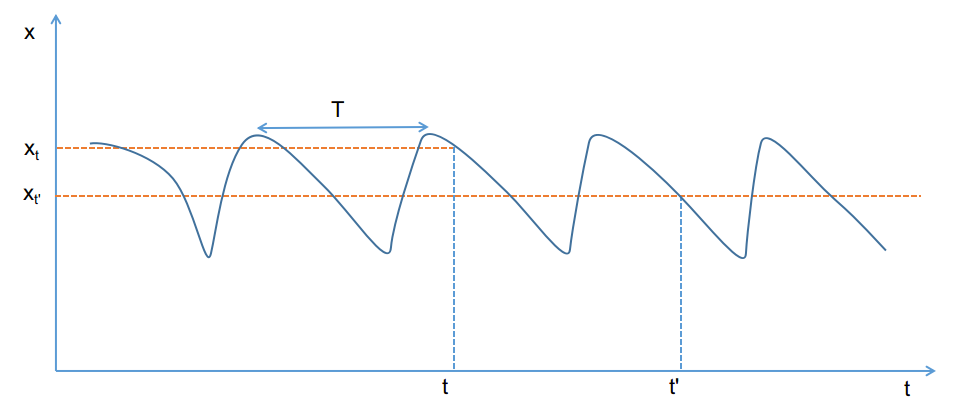
由于每次只能观测到一个面的装甲板,因此会产生锯齿状的波形,实际试验下来,用傅里叶变换得到的频谱并不明显。所以转向了一种更简单但是有效的办法:计算两个最高点之间的时间差。理论上,最高点可以用二阶导求得,但实际中采用了求一阶导然后找异常点的办法,也能获得很好的效果。找异常点是用了统计的方法。把那些与平均值的误差超过一定比率的标准差的点标为异常点。这样,就可以通过一段时间的连续观测,得到周期T了。
接下来的触发条件就和哨兵一样了,只是运动的预测从线性回归变成了周期重复:
\[| x_t - x_{t + t_{camera} + t_{process} + t_{shoot} + t_{fly}}| < \epsilon\]延迟的不稳定在这里会更加凸显。根据在打哨兵文章中的分析,$t_{camera}$的延迟稳定,$t_{process}$的延迟可以每次精确测量,而$t_{shoot}, t_{fly}$的延迟会变动上百毫秒。如果小陀螺的装甲板线速度有 1 m/s,就会造成十厘米的偏差,这样其实对于小装甲板还是不能提高击打效率。所以需要把发射部分的延迟调到一个相当稳定的值。
下面的视频是我们的调试过程,发射的延迟不太稳定,所以弹丸的落点不太精准,不过已经实现了基本功能:
总之,模型其实并不复杂,理清整个击打流程就可以找到判断时机的标准,最大的难点还是在于发射延迟的不稳定。

