一种四叉树的内存友好表示
在2021年春季学期的Advanced System Lab中,我们选择了图像压缩算法SPIHT进行性能优化,其中我为了优化编码过程中对于四叉树的访问,开发了一种全新的四叉树索引方式。
问题分析
SPIHT压缩分为两步,第一步是小波变换,将原图分离成横向细节、纵向细节、对角细节以及主要成分:

第二步是SPIHT编码,其中对于子节点的访问并不十分内存友好。从整体上看,编码的过程大体遵循从四叉树根部到叶子的顺序,反映到二维图像上,访问顺序就是从左上的主要成分,分散到其他三个方向上的细节:
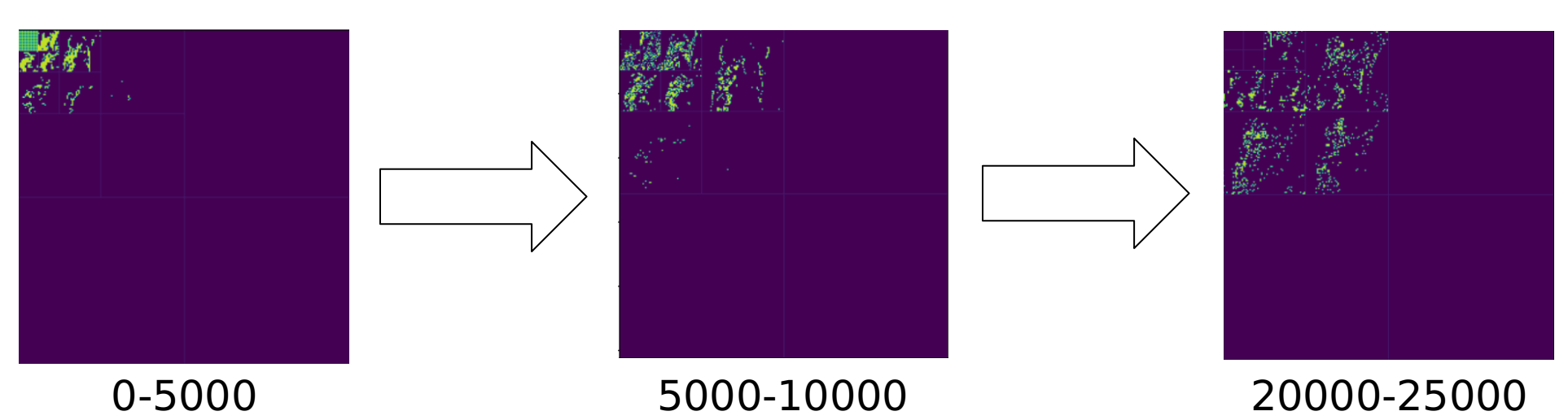
这对于实际上使用一维数组来储存的图像而言,几乎是随机访问,并不能享受到顺序访问带来的性能。
另一方面,对于每个节点的四个子节点的依次访问也是十分常见的操作,但是四个节点分布在 $2 \times 2$ 的小格子上,导致仅仅访问四个元素就会产生两次 cache miss,而如果这四个元素连续,就只需要一次 cache miss。所以,我们需要一种新的四叉树索引方式,来适应SPIHT的访问模式。
新的索引方式定义
让我们先考虑最简单的情况。如果只需要重排一个$2 \times 2$的块,如图中绿色块所示,那么把元素$y\times W+x, y\times W+x+1, (y+1)\times W +x, (y+1)\times W+x+1$(其中$W$是图片宽度)移动到$0,1,2,3$的位置即可。如果需要重排一个$4 \times 4$的数组(蓝色块),那么位于左上角$2 \times 2$块的父节点们可以按照之前$2\times 2$的块方式重排。为了保持四叉树的父子结构,元素$1,2,3$的子节点应该对应到元素$4,8,12$,这样中间的空隙刚好可以放下其他三个子节点,于是元素$4,8,12$的位置也确定了。对于剩下的三个子节点,可以按照$2 \times 2$块的方法局部重排。这样,我们就得到了一个完整的$4 \times 4$重排。
通过归纳,我们可以使用递归的方式定义出新的索引:
- 基础情况:对于$2 \times 2$块,直接按顺序重排;
- 递归:对于$2N \times 2N$块,首先将其分为四个$N \times N$块,并将其起始索引设置为$0, N^2, 2N^2, 3N^2$,然后使用$N \times N$块的重排方法,最后组合在一起。
通过这种递归,我们可以不断地拓展这种索引,直到足以容纳所需要处理的图片,就可以停止并继续接下来的编码过程了。
性能分析
对于整体的访问模式,左上角的元素都位于索引$\frac{1}{4} N^2$以下,其他三个方向的元素都位于索引$\frac{3}{4} N^2$以上,因此整体访问的模式可以近似于顺序访问。对于局部的四个子节点访问,现在四个元素在连续的空间上,因此最多只有一次cache miss,极大地减少了cache miss。同时,这种索引方式中,对于元素$i$的子节点访问简化为索引$4i,4i+1,4i+2,4i+3$,只需要一维索引来储存四叉树,可以进一步节省存储空间。
下面我们来看一下实验结果:
图中蓝色线是原始版本,红色线是使用新的四叉树索引的优化版本,仅仅通过优化内存组织形式,就可以减少50%的时间,同时性能上升到 6 IPC,接近 8 IPC的理论上限。
代码实现
我们使用C递归实现构建索引表:
static void build_rearrange_table(int *table, int width, int block, int cnt) {
if (block == 1) {
table[0] = cnt;
table[1] = cnt + 1;
table[width] = cnt + 2;
table[width + 1] = cnt + 3;
return;
}
build_rearrange_table(table, width, block / 2, cnt);
build_rearrange_table(table + block, width, block / 2, cnt + block * block);
build_rearrange_table(table + block * width, width, block / 2,
cnt + 2 * block * block);
build_rearrange_table(table + block * width + block, width, block / 2,
cnt + 3 * block * block);
}
table存放构建出来的索引表,width是索引表宽度,block是当前正在处理的块大小,cnt是索引。
利用这个索引表,可以重排整张图片:
static void rearrange_img(SPIHT *p_spiht, int *dst, int *src, int block) {
int lx = p_spiht->lx;
int ly = p_spiht->ly;
int width = p_spiht->width;
if (block == lx / 2) {
int *table = p_spiht->im_re_table;
for (int j = 0; j < ly; j++) {
for (int i = 0; i < lx; i++) {
dst[table[j * lx + i]] = src[j * width + i];
}
}
return;
}
rearrange_img(p_spiht, dst, src, block / 2);
rearrange_img(p_spiht, dst + 1 * block * block, src + block, block / 2);
rearrange_img(p_spiht, dst + 2 * block * block, src + block * width, block / 2);
rearrange_img(p_spiht, dst + 3 * block * block, src + block * width + block,
block / 2);
}
需要注意的是,在实际实现中,我们并没有创建一张和整张图像同等大小的索引表,因为在一次编码中,索引表只会使用一次,使用过大的索引表会造成浪费;我们只构建了最左上角图像块大小的索引表,然后使用递归的方式重排整张图片,并利用索引表提前返回,从而达到了索引表大小和递归深度的平衡。




